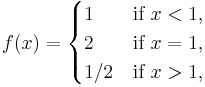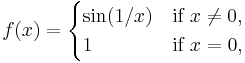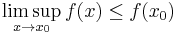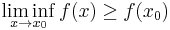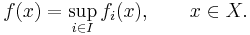Semi-continuity
- For the notion of upper or lower semicontinuous multivalued function see: Hemicontinuity
In mathematical analysis, semi-continuity (or semicontinuity) is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function f is upper (lower) semi-continuous at a point x0 if, roughly speaking, the function values for arguments near x0 are either close to f(x0) or less than (greater than) f(x0).
Contents |
Examples
Consider the function f, piecewise defined by f(x) = –1 for x < 0 and f(x) = 1 for x ≥ 0. This function is upper semi-continuous at x0 = 0, but not lower semi-continuous.
The indicator function of an open set is lower semi-continuous, whereas the indicator function of a closed set is upper semi-continuous. The floor function  , which returns the greatest integer less than or equal to a given real number x, is everywhere upper semi-continuous. Similarly, the ceiling function
, which returns the greatest integer less than or equal to a given real number x, is everywhere upper semi-continuous. Similarly, the ceiling function  is lower semi-continuous.
is lower semi-continuous.
A function may be upper or lower semi-continuous without being either left or right continuous. For example, the function
is upper semi-continuous at x = 1 although not left or right continuous. The limit from the left is equal to 1 and the limit from the right is equal to 1/2, both of which are different from the function value of 2. Similarly the function
is upper semi-continuous at x = 0 while the function limits from the left or right at zero do not even exist.
Let 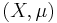 be a measure space and let
be a measure space and let 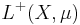 denote the set of positive measurable functions endowed with the topology of
denote the set of positive measurable functions endowed with the topology of  -almost everywhere convergence. Then the integral, seen as an operator from
-almost everywhere convergence. Then the integral, seen as an operator from 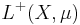 to
to ![[-\infty,%2B\infty]](/2012-wikipedia_en_all_nopic_01_2012/I/936cbe1fb6394ff85b26a5e76e81fcd5.png) is lower semi-continuous. This is just Fatou's lemma.
is lower semi-continuous. This is just Fatou's lemma.
Formal definition
Suppose X is a topological space, x0 is a point in X and f : X → R ∪ {–∞,+∞} is an extended real-valued function. We say that f is upper semi-continuous at x0 if for every ε > 0 there exists a neighborhood U of x0 such that f(x) ≤ f(x0) + ε for all x in U. For the particular case of a metric space, this can be expressed as
where lim sup is the limit superior (of the function f at point x0). (For non-metric spaces, an equivalent definition using nets may be stated.)
The function f is called upper semi-continuous if it is upper semi-continuous at every point of its domain. A function is upper semi-continuous if and only if {x ∈ X : f(x) < α} is an open set for every α ∈ R.
We say that f is lower semi-continuous at x0 if for every ε > 0 there exists a neighborhood U of x0 such that f(x) ≥ f(x0) – ε for all x in U. Equivalently, this can be expressed as
where lim inf is the limit inferior (of the function f at point x0).
The function f is called lower semi-continuous if it is lower semi-continuous at every point of its domain. A function is lower semi-continuous if and only if {x ∈ X : f(x) > α} is an open set for every α ∈ R; alternatively, a function is lower semi-continuous if and only if all of its lower levelsets {x ∈ X : f(x) ≤ α} are closed. Lower level sets are also called sublevel sets or trenches.[1]
Properties
A function is continuous at x0 if and only if it is upper and lower semi-continuous there. Therefore, semi-continuity can be used to prove continuity.
If f and g are two real-valued functions which are both upper semi-continuous at x0, then so is f + g. If both functions are non-negative, then the product function fg will also be upper semi-continuous at x0. Multiplying a positive upper semi-continuous function with a negative number turns it into a lower semi-continuous function.
If C is a compact space (for instance a closed, bounded interval [a, b]) and f : C → [–∞,∞) is upper semi-continuous, then f has a maximum on C. The analogous statement for (–∞,∞]-valued lower semi-continuous functions and minima is also true. (See the article on the extreme value theorem for a proof.)
Suppose fi : X → [–∞,∞] is a lower semi-continuous function for every index i in a nonempty set I, and define f as pointwise supremum, i.e.,
Then f is lower semi-continuous. Even if all the fi are continuous, f need not be continuous: indeed every lower semi-continuous function on a uniform space (e.g. a metric space) arises as the supremum of a sequence of continuous functions.
The indicator function of any open set is lower semicontinuous. The indicator function of a closed set is upper semicontinuous.
A function f : Rn→R is lower semicontinuous if and only if its epigraph (the set of points lying on or above its graph) is closed.
A function f : X→R, for some topological space X, is lower semicontinuous if and only if it is continuous with respect to the Scott topology on R.
References
- ^ Kiwiel, Krzysztof C. (2001). "Convergence and efficiency of subgradient methods for quasiconvex minimization". Mathematical Programming (Series A) (Berlin, Heidelberg: Springer) 90 (1): pp. 1-25. doi:10.1007/PL00011414. ISSN 0025-5610. MR1819784.
- Bourbaki, Nicolas (1998). Elements of Mathematics: General Topology, 1–4. Springer. ISBN 0201006367.
- Bourbaki, Nicolas (1998). Elements of Mathematics: General Topology, 5–10. Springer. ISBN 3540645632.
- Gelbaum, Bernard R.; Olmsted, John M.H. (2003). Counterexamples in analysis. Dover Publications. ISBN 0486428753.
- Hyers, Donald H.; Isac, George; Rassias, Themistocles M. (1997). Topics in nonlinear analysis & applications. World Scientific. ISBN 9810225342.